Yesterday, on #postgresql on irc some guy asked:
22:28 < rafasc> i am trying to use plpgsql to find the shortest path between two cities, each pair of cities has one or more edges, each edge has a different wheight. 22:28 < rafasc> Is there a easy way to compute the shortest path between two cities?
Well, I was not really in a mood to solve it, so I just told him to try with recursive queries, and went on my way.
But I thought about it. And decided to see if I can write the query.
To get some test data, I created two simple tables:
$ \d cities Table "public.cities" Column │ Type │ Modifiers ────────┼──────┼─────────── city │ text │ not null Indexes: "cities_pkey" PRIMARY KEY, btree (city) Referenced by: TABLE "routes" CONSTRAINT "routes_from_city_fkey" FOREIGN KEY (from_city) REFERENCES cities(city) TABLE "routes" CONSTRAINT "routes_to_city_fkey" FOREIGN KEY (to_city) REFERENCES cities(city) $ \d routes Table "public.routes" Column │ Type │ Modifiers ───────────┼─────────┼─────────── from_city │ text │ not null to_city │ text │ not null length │ integer │ not null Indexes: "routes_pkey" PRIMARY KEY, btree (from_city, to_city) Check constraints: "routes_check" CHECK (from_city < to_city) Foreign-key constraints: "routes_from_city_fkey" FOREIGN KEY (from_city) REFERENCES cities(city) "routes_to_city_fkey" FOREIGN KEY (to_city) REFERENCES cities(city)
Data in them is very simple:
$ select * from cities limit 5; city ──────────────── Vancouver Calgary Winnipeg Sault St Marie Montreal (5 rows) $ select * from routes limit 5; from_city │ to_city │ length ───────────┼───────────┼──────── Calgary │ Vancouver │ 3 Seattle │ Vancouver │ 1 Portland │ Seattle │ 1 Calgary │ Seattle │ 4 Calgary │ Helena │ 4 (5 rows)
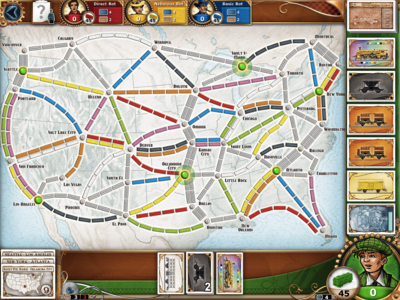
In case you wonder – the data represents base map for “Ticket to Ride" game – awesome thing, and if you haven't played it – get it, and play.
This map was part of review of the game on ars technica.
But anyway. So, I have 36 cities, and 78 unique paths between them, each with length information. So, with this I should be able to find the shortest path.
One word of warning though – the fact that it's possible to do in database, doesn't mean it's good idea. Personally, I think that it should be done in some standalone application, which would use some smarter algorithms, extensive cache, and so on. But – this is just a proof of concept, and the data size that I'm working on is small enough that it shouldn't matter.
Each route is stored only once in routes. So I'll start by duplicating the rows, so I will have them written “in both directions":
CREATE VIEW all_routes AS SELECT from_city, to_city, length FROM routes UNION ALL SELECT to_city, from_city, length FROM routes
This will save me some typing later on.
First, let's start with some small route, but one that will show that it actually works – Duluth-Toronto is great example.
Reason is very simple, We have these 3 routes:
from_city │ to_city │ length ────────────────┼────────────────┼──────── Duluth │ Sault St Marie │ 3 Sault St Marie │ Toronto │ 2 Duluth │ Toronto │ 6 (3 rows)
There is a direct connection (length 6), but it's actually cheaper to go via Sault St Marie, with total length of 5!
Here is a pause, of ~ 1 hour when I tried to write a query to solve my problem. And I failed. Kind of.
Query that would return the data is relatively simple:
WITH RECURSIVE multiroutes AS ( SELECT from_city, to_city, ARRAY[ from_city, to_city ] as full_route, length as total_length FROM all_routes WHERE from_city = 'Duluth' UNION ALL SELECT m.from_city, n.to_city, m.full_route || n.to_city, m.total_length + n.length FROM multiroutes m join all_routes n ON m.to_city = n.from_city WHERE n.to_city <> ALL( m.full_route ) ) SELECT * FROM multiroutes WHERE to_city = 'Toronto' ORDER BY total_length desc limit 1;
But the problem is – it's extremely slow. And uses a lot of resources, which made OOM killer in my desktop to kill it (yes, stupid OOM killer).
I tried to implement simple pruning of searched paths if they are longer than current shortest on given route, but I couldn't find a way to do it – it seems to require subselect, and subselects referring to recursive queries, are not allowed within the recursive query itself.
(I think that perhaps RhodiumToad (on irc) can do it in a single query, but I'm far away from his level of skills, so I had to pass)
Does that mean it can't be done in database? No.
Luckily, we have functions. And functions can be rather smart.
To make the function simpler to use and write, I defined a type:
CREATE TYPE route_dsc as ( from_city TEXT, to_city TEXT, full_route TEXT[], total_length INT4 );
This is a quite easy way to encapsulate all information about a single route as somewhat scalar value.
Now, I can write the function:
CREATE OR REPLACE FUNCTION
get_shortest_route( p_from TEXT, p_to TEXT )
RETURNS SETOF route_dsc AS
$$
DECLAREsanity_count INT4;
final_routes route_dsc[];
current_routes route_dsc[];
r route_dsc;
BEGINSELECT count(*) INTO sanity_count
FROM citiesWHERE city in (p_from, p_to);
IF sanity_count <> 2 THEN
raise exception 'These are NOT two, distinct, correct city names.';END IF;
current_routes := array(
SELECT row(from_city, to_city, ARRAY[from_city, to_city], length)
FROM all_routesWHERE from_city = p_from
);final_routes := current_routes;LOOP
current_routes := array(
SELECT row(
c.from_city,
a.to_city,
c.full_route || a.to_city,
c.total_length + a.length)
FROMunnest( current_routes ) as c
join all_routes a on c.to_city = a.from_city
WHEREa.to_city <> all( c.full_route )
ANDc.total_length + a.length <= least(
coalesce(
(SELECT min(l.total_length)
FROM unnest( final_routes ) as l
WHERE ( l.from_city, l.to_city ) = (c.from_city, p_to)
),
c.total_length + a.length
),
coalesce(
(SELECT min(l.total_length)
FROM unnest( final_routes ) as l
WHERE ( l.from_city, l.to_city ) = (c.from_city, a.to_city)
),
c.total_length + a.length
)));EXIT WHEN current_routes = '{}';
final_routes := final_routes || current_routes;
END LOOP;RETURN queryWITH rr as (
SELECTfrom_city,to_city,full_route,total_length,dense_rank()
over (partition BY from_city, to_city ORDER BY total_length) as rank
FROM unnest( final_routes )
WHERE from_city = p_from AND to_city = p_to
)SELECT from_city, to_city, full_route, total_length FROM rr where rank = 1;
RETURN;END;$$ language plpgsql;
Looks huge, but in fact it's only because there are many queries inside. So, let's see what the function does:
- lines 1-4 – standard preamble with function name, 2 arguments (cities we want to connect), and information that we will be returning set of records based on the type I just defined. In here you might wonder – why set of? We want just the shortest route. Yes, that's correct but it's perfectly possible (and very common) that there are many rows with the same, minimal length. So, instead of picking one randomly – I will return them all.
- lines 6-9 – variable declarations, not really interesting
- lines 11-16 – sanity check. Simple verification that both given names are city names, and that they are different.
- lines 18-22 – I build current_routes based on all routes coming from source city. For example, If I'd call the function to find me route from Duluth to Toronto, the array would get these rows:
$ SELECT from_city, to_city, ARRAY[from_city, to_city], length FROM all_routes WHERE from_city = 'Duluth'; from_city │ to_city │ array │ length ───────────┼────────────────┼───────────────────────────┼──────── Duluth │ Helena │ {Duluth,Helena} │ 6 Duluth │ Winnipeg │ {Duluth,Winnipeg} │ 4 Duluth │ Sault St Marie │ {Duluth,"Sault St Marie"} │ 3 Duluth │ Toronto │ {Duluth,Toronto} │ 6 Duluth │ Omaha │ {Duluth,Omaha} │ 2 Duluth │ Chicago │ {Duluth,Chicago} │ 3 (6 rows)
- line 23 – I copy current_routes to “final_routes". current_routes contains only routes that the loop below has to work on, but final routes – is an array of all routes that will be used for finding final solution
- lines 25-59 – basically infinite loop (of course with proper exit condition), which recursively finds routes:
- lines 26-56 – core of the function. This query builds new list of routes, based on what's in current_routes, with following criteria:
- new route must be from a city that is at the end of some route in “current_routes" (i.e. it's next segment for multi-city route
- added (to route) city cannot be already in full_route (there is no point in revisiting cities when we're looking for shortest path
- new total length of route (i.e. some route from current_routes + new segment) has to be shorter (or the same) as existing shortest path between these two cities. By “these" I mean original “from" city, and newly added “to" city. So, if we already have a route between cities “a" and “b" that is “10" long, there is no point in adding new route that is “20" long.
- similar condition as above, but checking against already found requested route – i.e. route between cities user requested in passing arguments
- above two criteria make sense only if there are matching routes already in final_routes – hence the need for coalesce()
All such routes are stored in current_routes for future checking
- line 57 – if the query above didn't return any routes – we're done, can exit the loop
- line 58 – if there are some routes – add them to final_routes, and repeat the loop
- lines 26-56 – core of the function. This query builds new list of routes, based on what's in current_routes, with following criteria:
- lines 60-72 – return of the important data. I take all the routes in final_routes, from there, pick only the ones that match from_city/to_city with parameters given on function call, and then I use dense_rank() to find all records that have minimal total_length. All these records will get returned.
If that's complex, let me show you an example. What is stored, in which variable, at which step, when finding the route from Duluth to Toronto.
- after line 23 in function, both current_routes and final_routes contain:
from_city to_city total_length full_route Duluth Helena 6 {Duluth,Helena} Duluth Winnipeg 4 {Duluth,Winnipeg} Duluth Sault St Marie 3 {Duluth,"Sault St Marie"} Duluth Toronto 6 {Duluth,Toronto} Duluth Omaha 2 {Duluth,Omaha} Duluth Chicago 3 {Duluth,Chicago} - First run of the main recursive query – at line 57 current_routes are:
from_city to_city total_length full_route Duluth Toronto 5 {Duluth,"Sault St Marie",Toronto} Duluth Pittsburg 6 {Duluth,Chicago,Pittsburg} Duluth Saint Louis 5 {Duluth,Chicago,"Saint Louis"} Duluth Denver 6 {Duluth,Omaha,Denver} Duluth Kansas City 3 {Duluth,Omaha,"Kansas City"} and since it's obviously not empty set – it continues.
Please note that it didn't (for example) add route Duluth – Helena – Seattle (which is correct route, as you can see on the image above). Reason is very simple – we already found one route Duluth – Toronto, and its length is 6, so adding new route which is longer than this – doesn't make sense. - At line 58 final_routes are set to:
from_city to_city total_length full_route Duluth Helena 6 {Duluth,Helena} Duluth Winnipeg 4 {Duluth,Winnipeg} Duluth Sault St Marie 3 {Duluth,"Sault St Marie"} Duluth Toronto 6 {Duluth,Toronto} Duluth Omaha 2 {Duluth,Omaha} Duluth Chicago 3 {Duluth,Chicago} Duluth Toronto 5 {Duluth,"Sault St Marie",Toronto} Duluth Pittsburg 6 {Duluth,Chicago,Pittsburg} Duluth Saint Louis 5 {Duluth,Chicago,"Saint Louis"} Duluth Denver 6 {Duluth,Omaha,Denver} Duluth Kansas City 3 {Duluth,Omaha,"Kansas City"} Which is simply previous final_routes with added new 5.
- After next iteration of the loop, based on 5-element current_routes, we got only two new routes:
from_city to_city total_length full_route Duluth Oklahoma City 5 {Duluth,Omaha,"Kansas City","Oklahoma City"} Duluth Saint Louis 5 {Duluth,Omaha,"Kansas City","Saint Louis"} And of course they got added to final_routes.
- another iteration of the loop, based on current_routes with just two elements – didn't return any rows. There simply is no way to extend routes “Duluth-Omaha-Kansas City" or “Duluth-Omaha-Saint Louis" in a way that wouldn't extend already found route “Duluth-Sault St Marie-Toronto" with length 5.
- Since this iteration of loop didn't find anything, loop exits, and the final_routes contains:
from_city to_city total_length full_route Duluth Helena 6 {Duluth,Helena} Duluth Winnipeg 4 {Duluth,Winnipeg} Duluth Sault St Marie 3 {Duluth,"Sault St Marie"} Duluth Toronto 6 {Duluth,Toronto} Duluth Omaha 2 {Duluth,Omaha} Duluth Chicago 3 {Duluth,Chicago} Duluth Toronto 5 {Duluth,"Sault St Marie",Toronto} Duluth Pittsburg 6 {Duluth,Chicago,Pittsburg} Duluth Saint Louis 5 {Duluth,Chicago,"Saint Louis"} Duluth Denver 6 {Duluth,Omaha,Denver} Duluth Kansas City 3 {Duluth,Omaha,"Kansas City"} Duluth Oklahoma City 5 {Duluth,Omaha,"Kansas City","Oklahoma City"} Duluth Saint Louis 5 {Duluth,Omaha,"Kansas City","Saint Louis"}
Based on the final_routes above, query in lines 61-72 calculates correct answer, and shows it.
OK. So it works. But how slow it is?
First, let's start with very simple example – Atlanta – Nashville. These two cities are connected using a single one-element route. Call to function:
$ SELECT * FROM get_shortest_route('Atlanta', 'Nashville'); from_city │ to_city │ full_route │ total_length ───────────┼───────────┼─────────────────────┼────────────── Atlanta │ Nashville │ {Atlanta,Nashville} │ 1 (1 row) Time: 1.045 ms
What about the Duluth-Toronto?
$ SELECT * FROM get_shortest_route('Duluth', 'Toronto'); from_city │ to_city │ full_route │ total_length ───────────┼─────────┼───────────────────────────────────┼────────────── Duluth │ Toronto │ {Duluth,"Sault St Marie",Toronto} │ 5 (1 row) Time: 2.239 ms
Something longer perhaps:
$ SELECT * FROM get_shortest_route('Duluth', 'Los Angeles'); from_city │ to_city │ full_route │ total_length ───────────┼─────────────┼───────────────────────────────────────────────────────────────────────────────┼────────────── Duluth │ Los Angeles │ {Duluth,Omaha,Denver,Phoenix,"Los Angeles"} │ 14 Duluth │ Los Angeles │ {Duluth,Omaha,Denver,"Santa Fe",Phoenix,"Los Angeles"} │ 14 Duluth │ Los Angeles │ {Duluth,Omaha,"Kansas City","Oklahoma City","Santa Fe",Phoenix,"Los Angeles"} │ 14 Duluth │ Los Angeles │ {Duluth,Helena,"Salt Lake City","Las Vegas","Los Angeles"} │ 14 Duluth │ Los Angeles │ {Duluth,Omaha,Denver,"Salt Lake City","Las Vegas","Los Angeles"} │ 14 (5 rows)
And how about a cross country?
$ SELECT * FROM get_shortest_route('Vancouver', 'Miami'); from_city │ to_city │ full_route │ total_length ───────────┼─────────┼──────────────────────────────────────────────────────────────────────────────────────┼────────────── Vancouver │ Miami │ {Vancouver,Calgary,Helena,Omaha,"Kansas City","Saint Louis",Nashville,Atlanta,Miami} │ 23 Vancouver │ Miami │ {Vancouver,Seattle,Helena,Omaha,"Kansas City","Saint Louis",Nashville,Atlanta,Miami} │ 23 (2 rows) Time: 62.507 ms
The longer the road the more time it takes to find it. Which is pretty understandable.
So, to wrap it. It can be done in database. It is not as slow as I expected. I wasn't able to find a way to do it without functions, but it might be possible for someone smarter than me.
And I still don't think it's a good idea to put this logic in database.
Could you share the TTR route data for testing? I suspect your problem is that you used “UNION ALL” instead of “UNION” in your recursive query. But I’m too lazy to enter all that data by hand. 🙂
https://www.depesz.com/wp-content/uploads/2012/06/ttr.dump.gz
Isn’t ðis easier & faster wiþ recursive WITH queries?
@Leonadro:
did you read the blogpost?
I wrote, at least twice, that I tried, but couldn’t make it. If you can provide such query – I will gladly see/review it.
Hell,
You will find a query implementing such thing with WITH RECURSIVE in the .zip file available here: http://www.postgresql-sessions.org/_media/requetes_sessions_postgresql.zip
It was done by my ex-coworker Jean-Michel Souchard.
Hello… sorry for the typo…
@Thomas:
downloaded, and grep’ped for RECURSIVE – but it’s not in english, so I can’t really find out which of the queries you have in mind.
There’s a SQL file with Dijkstra in its filename 😉
Hmm. Indeed, after working over this, there’s no way to do it with recursive queries. The problem is that the key piece of information that lets you cut you search short is knowing the best currently-known length for a given route. And that sort of information simply isn’t available via WITH RECURSIVE, since that mechanism works purely iteratively based on either UNION or UNION ALL.
Interestingly, you *can* use the same iterative technique to solve the problem directly, much like you might have done before WITH RECURSIVE to generate transitive closures:
create temporary table full_routes (
from_city text, to_city text, length numeric, path text[]
);
— base case
insert into full_routes
select r.from_city, r.to_city, r.length, array [ r.from_city, r.to_city ]
from all_routes r;
— repeat the following two steps until insertion inserts zero rows
— add new routes only if they are shorter than the current route
insert into full_routes
select f.from_city, r.to_city, f.length + r.length, f.path || r.to_city
from all_routes r, full_routes f
where r.from_city = f.to_city
and r.to_city all ( f.path )
and f.length + r.length (select min(f2.length) from full_routes f2
where f.from_city = f2.from_city
and f.to_city = f2.to_city);
This method *is* able to use the length to decide when to stop, and therefore generates many many less possible routes than recursive method, which must keep going and going, generating many billions of paths and running out of memory. (There are only 1616 shortest paths between cities, counting both directions of each route, but you can easily demonstrate that the recursive query generates at least millions by running the query with progressively higher LIMIT clauses.)
I’m rather sad to see that WITH RECURSIVE can’t be used to run something as simple as a depth-first search with weighted edges. I hadn’t realized it was that limited. But, at least it does take care of some basic graph problems.
After puzzling over the link from Mr. Reiss: This file appears to implement exactly the same method that is included in the blog post above, and on a sufficiently connected graph it would fail the same way. It must enumerate every possible path through the graph before eliminating any.
@Thomas:
Got your translation in mail – still – the query uses columns which I don’t quite understand (cp_deb/cp_fin).
Plus – this is *very* slow. For the 12 edges it has it takes over 2ms to calculate on my machine.
Maybe I’m doing something wrong – but can you try to modify the query, and run it on my dataset (it’s linked in a comment) to try to find the routes Duluth-Toronto and Vancouver-Miami?
@Thomas:
re the comment from J. Prevost – are you sure this is different approach? If what J. Prevost wrote is true – well, I did it, and it works, but it’s too slow for any use.
The major problem is that there is no logic to prune obviously wrong routes.
I think the cp_deb and cp_fin are simply secondary parts of the keys for locations. The point of departure and the destination are specified by (ville_deb, cp_deb) and (ville_fin, cp_fin), respectively.
Hi Depesz,
I often read your blog and I had a little think about this. I’m not very experienced with CTEs/Window functions let alone the recursive form, but after loading your generously keyed data, I came up with this (seems quick to me)
I'm using:
PostgreSQL 9.1.4 on x86_64-unknown-linux-gnu, compiled by gcc (Ubuntu/Linaro 4.6.3-1ubuntu5) 4.6.3, 64-bit
Seems it removed my from between n.to_city and ALL
Great post!
PS Hubert, which SQL highlighter do you use for your posts?
@Pavel:
WP-Syntax plugin. It uses GeSHi, afaik.
@Mark:
Is there a (not equal to) missing between “n.to_city” and “ALL( m.full_route)” in your query? I added it and then it works. Where should the “from between n.to_city and ALL” be inserted? That’s not valid syntax either, perhaps it removed some characters in your comment?
Your query takes 2264ms while Depesz function for the same route takes 71ms, not that fast, but it works.
Have you tried pgRouting? It has shortest path and traveling salesman.
@Stephen Mather:
pgRouting relies on C functions, the implementation is not in SQL or PL/pgSQL.
Hi Depesz,
Apparently I was trying an approach very similar to yours. Even without having a sub-query to get the best distance so far, this is still useful since it prunes all the edges after the destination is matched.
with recursive t(src, dest, edge, route, distance, best_distance)
as
(
— Source city, Target City, Current City (initially the Source City), Cumulative route (initially only Source City), Cumulative Distance, Best Distance
select ‘a’, ‘e’, ‘a’, ‘{“a”}’::text[], 0, 2147483647
union all
select t.src, t.dest, r.city2, route || array[r.city2], t.distance + r.distance,
case when t.dest = r.city2 then least(t.distance + r.distance, t.best_distance) else t.best_distance end
from t
join test.route2 r on r.city1 = t.edge and not(r.city2 = any(route)) and t.distance + r.distance < best_distance
)
select *
from t
where t.route[array_upper(t.route, 1)] = 'e' — Compare to Destination City
order by distance asc
limit 1;
Where the data is created using this:
create table test.route
(
city1 text,
city2 text,
distance int
);
insert into test.route values
('a', 'b', 5),
('b', 'c', 4),
('b', 'h', 2),
('c', 'h', 3),
('c', 'd', 5),
('d', 'e', 3),
('e', 'f', 2),
('e', 'a', 5),
('f', 'g', 1),
('f', 'a', 2);
create view test.route2
as
select city1, city2, distance
from test.route
union all
select city2, city1, distance
from test.route;
@Mark:
ok. got the time to analyze your query.
It’s really nice, but with larger datasets the performance will degrade.
Reason is very simple – min_solve doesn’t propagate to next iterations of the recursive query.
It can be easily visible when you’ll change findpath CTE to be:
SELECT ‘Helena’::TEXT as from_city, ‘Toronto’::TEXT as to_city
and then make the final query, instead of querying solution:
SELECT * FROM multiroutes WHERE 2 = array_upper(full_route, 1) ORDER BY full_route;
then run the query, increment “2=”, rerun, and so on.
With 3= – we see that all rows have min_solve = 12.
with 4= – it correctly finds shorter path – 11 elements.
but then – 5= min_solve is again null.
Of course your condition in join in multiroute CTE did excellent job at filtering out paths – so it can actually finish finding even longest paths in my TTR example, but if the map was larger – it would lag pretty badly.
We can see, that when searching for Duluth-Toronto, final multiroute CTE contains 125 routes.
On the other hand – my function, for the same path, has at most 13.
A bit longer trip – Helena-Toronto – your query considers 304 paths, function – 47.
For the long, cross-continent route – Vancouver-Miami – query considers 27677 routes, function – 243.
Still – all that aside – I bow before your skill – it is great application of window functions and CTE.
@Tzvi:
I reformatted your query, and modified it so that it works not against your test table, but against the tables that I used in this blogpost:
Result – definitely not good. Started it, and killed after ~ 10 seconds, with no results. Sorry – it might behave nicely when you have 10 routes, but it doesn’t work when you have more.
Well, I had a little bit more of a think about it, and whilst not as few paths as the function solution, there is a significant reduction in the search tree.
The main difference here is the tracking of the best path length for the to_city in the multiroutes CTE and using that to limit which new paths are added to the search tree. This brings the intermediate search space down to approx 2300 rows instead of the nearly 28000. It also reduced my execution time from 1300ms down to 200ms (warm).
It has been an interesting exercise in using SQL to solve a problem.
@Mark:
WOW again. This query ran for me, for the Vancouver-Miami route in 21ms (my function needed ~70!). And this is done while still taking into consideration 2282 routes (10 times as many as function).
But – as good as it is, I think I found a way to make it faster:
Took (best result); 9.5ms for Vancouver-Miami, and it considered only 847 routes.
The difference is usage of least() for calculation of min_solve to prevent reappearance of “null” in min_solve column for next iterations of loop.
I always forget about least and greatest 🙂
Now how do I get the query code in iterative commits between Mark and Depesz into a github repo (just starting out learning SQL queries, but am familiar with Dikstra’s alg and A*s
Splendid post and comments
I’ll attempt to do justice to the post and the iterative query updates at https://github.com/victusfate/FriendlySQL
Ok you can see the relative commits and history of the query here (the diff view was helpful to me since I’m not as quick to notice differences in the text/comments)
Mark Guyatt’s first version:
https://github.com/victusfate/FriendlySQL/blob/8b74560661f4ba8efc1ee70d3c7f9e3fd282f1c7/MarkGuyattDepeszShortestPathQuery.sql
Mark’s second version after Depesz comments:
https://github.com/victusfate/FriendlySQL/commit/69b3ee56f04fc825d5e6cbbd9adabba23984d1e2
Depesz updates:
https://github.com/victusfate/FriendlySQL/commit/abba78b6b42608994383759eb07a06c610b0741d
Very cool.